How To Find Work Done By Friction

Work, Energy, and Free energy Resource

43 Kinetic Free energy and the Work-Energy Theorem

Learning Objectives

Explain work every bit a transfer of free energy and net piece of work every bit the work done by the net forcefulness.
Explicate and utilize the work-free energy theorem.

Work Transfers Energy

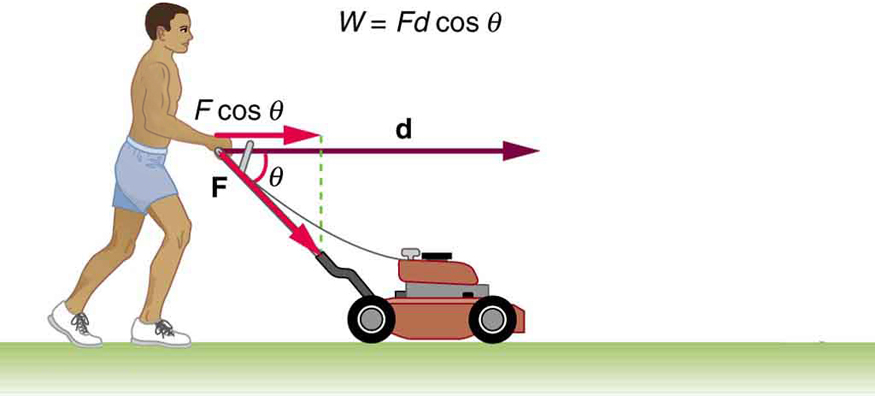
What happens to the work done on a system? Energy is transferred into the system, but in what form? Does it remain in the system or motion on? The answers depend on the situation. For example, if the lawn mower in (Figure)(a) is pushed just hard plenty to keep it going at a constant speed, then energy put into the mower by the person is removed continuously by friction, and eventually leaves the arrangement in the form of rut transfer. In contrast, piece of work done on the briefcase past the person carrying it up stairs in (Figure)(d) is stored in the briefcase-World system and can be recovered at any time, as shown in (Figure)(e). In fact, the edifice of the pyramids in ancient Arab republic of egypt is an example of storing energy in a organization by doing piece of work on the organisation. Some of the energy imparted to the rock blocks in lifting them during construction of the pyramids remains in the stone-Earth system and has the potential to do work.

In this section we begin the report of various types of work and forms of free energy. We will find that some types of work get out the energy of a arrangement abiding, for example, whereas others modify the organisation in some manner, such as making it movement. We will too develop definitions of important forms of free energy, such as the energy of motion.

Net Piece of work and the Piece of work-Free energy Theorem

We know from the report of Newton's laws in Dynamics: Forcefulness and Newton'south Laws of Motility that internet force causes acceleration. We will see in this section that work washed past the cyberspace force gives a system energy of motion, and in the procedure we will too find an expression for the free energy of motility.

Let u.s. first by because the total, or net, work done on a system. Net work is defined to be the sum of work washed by all external forces—that is, net work is the work done past the net external force ${\mathbf{F}}_{\text{net}}$ . In equation form, this is ${W}_{\text{net}}={F}_{\text{net}}d\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta$ where $\theta$ is the bending betwixt the force vector and the displacement vector.

(Figure)(a) shows a graph of force versus displacement for the component of the forcefulness in the direction of the displacement—that is, an $F\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta$ vs. $d$ graph. In this case, $F\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta$ is constant. Y'all can see that the area nether the graph is $Fd\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta$ , or the piece of work done. (Figure)(b) shows a more than general process where the force varies. The expanse under the curve is divided into strips, each having an average strength $\left(F\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta {\right)}_{i\left(\text{ave}\right)}$ . The work done is $\left(F\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta {\right)}_{i\left(\text{ave}\right)}{d}_{i}$ for each strip, and the full work washed is the sum of the ${W}_{i}$ . Thus the total work washed is the total area under the curve, a useful belongings to which we shall refer afterwards.

Cyberspace work will be simpler to examine if we consider a one-dimensional situation where a forcefulness is used to accelerate an object in a management parallel to its initial velocity. Such a situation occurs for the packet on the roller belt conveyor system shown in (Effigy).

A package on a roller belt is pushed horizontally through a distance $\mathbf{d}$ .

The strength of gravity and the normal strength interim on the package are perpendicular to the displacement and do no work. Moreover, they are also equal in magnitude and opposite in management then they cancel in calculating the cyberspace forcefulness. The net force arises solely from the horizontal applied forcefulness ${\mathbf{F}}_{\text{app}}$ and the horizontal friction force $\mathbf{f}$ . Thus, as expected, the cyberspace strength is parallel to the deportation, so that $\theta =0º$ and $\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta =1$ , and the internet work is given past

${W}_{\text{net}}={F}_{\text{net}}d.$

The effect of the net force ${\mathbf{F}}_{\text{net}}$ is to advance the parcel from ${v}_{0}$ to $v$ . The kinetic free energy of the packet increases, indicating that the net piece of work done on the arrangement is positive. (Come across (Figure).) By using Newton's second law, and doing some algebra, nosotros can reach an interesting decision. Substituting ${F}_{\text{net}}=\text{ma}$ from Newton's second law gives

${W}_{\text{net}}=\text{mad.}$

To go a relationship between net work and the speed given to a system past the internet force acting on it, nosotros take $d=x-{x}_{0}$ and use the equation studied in Motion Equations for Constant Acceleration in 1 Dimension for the change in speed over a altitude $d$ if the acceleration has the constant value $a$ ; namely, ${v}^{2}={{v}_{0}}^{2}+2\text{ad}$ (annotation that $a$ appears in the expression for the net piece of work). Solving for acceleration gives $a=\frac{{v}^{2}-{{v}_{0}}^{2}}{2d}$ . When $a$ is substituted into the preceding expression for ${W}_{\text{net}}$ , we obtain

${W}_{\text{net}}=m\left(\frac{{v}^{2}-{{v}_{0}}^{2}}{2d}\right)d.$

The $d$ cancels, and we rearrange this to obtain

$W{}_{\text{net}}\text{}=\frac{1}{2}{\text{mv}}^{2}-\frac{1}{2}{\text{mv}}_{0}^{ 2}\text{.}$

This expression is called the work-energy theorem, and it really applies in general (even for forces that vary in direction and magnitude), although we have derived it for the special case of a abiding force parallel to the deportation. The theorem implies that the cyberspace work on a organisation equals the change in the quantity $\frac{1}{2}{\text{mv}}^{2}$ . This quantity is our outset example of a form of energy.

The Work-Free energy Theorem

The net work on a system equals the change in the quantity $\frac{1}{2}{\text{mv}}^{2}$ .

${W}_{\text{net}}=\frac{1}{2}{\text{mv}}^{2}-\frac{1}{2}{\text{mv}}_{0}^{ 2}$

The quantity $\frac{1}{2}{\text{mv}}^{2}$ in the work-free energy theorem is divers to exist the translational kinetic free energy (KE) of a mass $m$ moving at a speed $v$ . (Translational kinetic energy is distinct from rotational kinetic energy, which is considered later.) In equation form, the translational kinetic energy,

$\text{KE}=\frac{1}{2}{\text{mv}}^{2},$

is the energy associated with translational motion. Kinetic energy is a form of free energy associated with the motion of a particle, unmarried body, or system of objects moving together.

We are aware that it takes energy to go an object, like a car or the package in (Figure), up to speed, only it may be a fleck surprising that kinetic energy is proportional to speed squared. This proportionality means, for example, that a motorcar traveling at 100 km/h has four times the kinetic free energy it has at l km/h, helping to explain why loftier-speed collisions are so devastating. We volition now consider a serial of examples to illustrate various aspects of work and free energy.

Calculating the Kinetic Energy of a Package

Suppose a 30.0-kg package on the roller belt conveyor system in (Effigy) is moving at 0.500 thou/s. What is its kinetic free energy?

Strategy

Considering the mass $m$ and speed $v$ are given, the kinetic energy can be calculated from its definition as given in the equation $\text{KE}=\frac{1}{2}{\text{mv}}^{2}$ .

Solution

The kinetic free energy is given by

$\text{KE}=\frac{1}{2}{\text{mv}}^{2}\text{.}$

Entering known values gives

$\text{KE}=0\text{.}5\left(\text{30.0 kg}\right)\left(\text{0.500 m/s}{\right)}^{2},$

which yields

$\text{KE}=\text{3.75 kg}\cdot {m}^{2}{\text{/s}}^{2}=\text{3.75 J.}$

Discussion

Note that the unit of kinetic energy is the joule, the same as the unit of work, as mentioned when work was kickoff defined. It is also interesting that, although this is a fairly massive package, its kinetic energy is not big at this relatively low speed. This fact is consistent with the observation that people can move packages like this without exhausting themselves.

Determining the Work to Accelerate a Packet

Suppose that you button on the 30.0-kg parcel in (Figure) with a constant forcefulness of 120 Due north through a distance of 0.800 m, and that the opposing friction force averages five.00 Northward.

(a) Calculate the net piece of work done on the package. (b) Solve the same problem equally in part (a), this time by finding the work done by each force that contributes to the net force.

Strategy and Concept for (a)

This is a motion in one dimension problem, because the downward force (from the weight of the package) and the normal force have equal magnitude and opposite direction, so that they abolish in calculating the net forcefulness, while the applied forcefulness, friction, and the displacement are all horizontal. (See (Figure).) As expected, the net piece of work is the net force times distance.

Solution for (a)

The net forcefulness is the push button strength minus friction, or ${F}_{\text{net}}\text{= 120 N - 5}\text{.}\text{00 N = 115 N}$ . Thus the net work is

$\begin{array}{lll}{W}_{\text{net}}& =& {F}_{\text{net}}d=\left(\text{115 N}\right)\left(\text{0.800 m}\right)\\ & =& \text{92.0 N}\cdot m=\text{92.0 J.}\end{array}$

Word for (a)

This value is the net piece of work washed on the package. The person actually does more work than this, considering friction opposes the motion. Friction does negative work and removes some of the energy the person expends and converts it to thermal energy. The net work equals the sum of the piece of work done by each individual force.

Strategy and Concept for (b)

The forces acting on the bundle are gravity, the normal strength, the force of friction, and the applied force. The normal force and force of gravity are each perpendicular to the displacement, and therefore exercise no piece of work.

Solution for (b)

The applied forcefulness does work.

$\begin{array}{lll}{W}_{\text{app}}& =& {F}_{\text{app}}d\phantom{\rule{0.25em}{0ex}}\text{cos}\left(0º\right)={F}_{\text{app}}d\\ & =& \left(\text{120 N}\right)\left(\text{0.800 m}\right)\\ & =& \text{96.0 J}\end{array}$

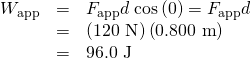
The friction forcefulness and displacement are in opposite directions, so that $\theta =\text{180º}$ , and the piece of work done by friction is

$\begin{array}{lll}{W}_{\text{fr}}& =& {F}_{\text{fr}}d\phantom{\rule{0.25em}{0ex}}\text{cos}\left(\text{180º}\right)=-{F}_{\text{fr}}d\\ & =& -\left(\text{5.00 N}\right)\left(\text{0.800 m}\right)\\ & =& -\text{4.00 J.}\end{array}$

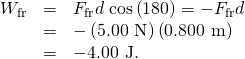
And then the amounts of work done past gravity, by the normal force, by the applied force, and by friction are, respectively,

$\begin{array}{lll}{W}_{\text{gr}}& =& 0,\\ {W}_{N}& =& 0,\\ {W}_{\text{app}}& =& \text{96.0 J,}\\ {W}_{\text{fr}}& =& -\text{4.00 J.}\end{array}$

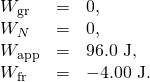
The total work done every bit the sum of the piece of work done past each force is then seen to exist

${W}_{\text{total}}={W}_{\text{gr}}+{W}_{N}+{W}_{\text{app}}+{W}_{\text{fr}}=\text{92}\text{.0 J}.$

Discussion for (b)

The calculated total work ${W}_{\text{total}}$ as the sum of the work by each force agrees, as expected, with the piece of work ${W}_{\text{net}}$ done by the net force. The piece of work washed by a drove of forces interim on an object tin can be calculated by either approach.

Determining Speed from Work and Free energy

Find the speed of the bundle in (Figure) at the finish of the push, using piece of work and energy concepts.

Strategy

Here the work-energy theorem tin can be used, because we accept merely calculated the internet work, ${W}_{\text{net}}$ , and the initial kinetic energy, $\frac{1}{2}{m{v}_{0}}^{2}$ . These calculations allow usa to find the terminal kinetic energy, $\frac{1}{2}{\text{mv}}^{2}$ , and thus the concluding speed $v$ .

Solution

The piece of work-free energy theorem in equation form is

${W}_{\text{net}}=\frac{1}{2}{\text{mv}}^{2}-\frac{1}{2}{m{v}_{0}}^{2}\text{.}$

Solving for $\frac{1}{2}{\text{mv}}^{2}$ gives

$\frac{1}{2}{\text{mv}}^{\text{2}}={W}_{\text{net}}+\frac{1}{2}{m{v}_{0}}^{2}\text{.}$

Thus,

$\frac{1}{2}{\text{mv}}^{2}=\text{92}\text{.}0 J+3\text{.}\text{75 J}=\text{95.}\text{75 J.}$

Solving for the final speed as requested and entering known values gives

$\begin{array}{lll}v& =& \sqrt{\frac{2\text{(95.75 J)}}{m}}=\sqrt{\frac{\text{191.5 kg}\cdot {m}^{2}{\text{/s}}^{2}}{\text{30.0 kg}}}\\ & =& \text{2.53 m/s.}\end{array}$

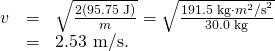
Give-and-take

Using work and energy, we not only arrive at an reply, we run into that the last kinetic energy is the sum of the initial kinetic free energy and the net work washed on the packet. This means that the work indeed adds to the energy of the bundle.

Work and Energy Can Reveal Distance, Too

How far does the package in (Figure) coast later on the push, assuming friction remains constant? Use piece of work and energy considerations.

Strategy

Nosotros know that once the person stops pushing, friction volition bring the bundle to rest. In terms of energy, friction does negative work until it has removed all of the package's kinetic free energy. The work done by friction is the force of friction times the distance traveled times the cosine of the bending between the friction strength and deportation; hence, this gives united states of america a way of finding the altitude traveled afterwards the person stops pushing.

Solution

The normal force and force of gravity cancel in computing the net strength. The horizontal friction force is so the cyberspace forcefulness, and information technology acts contrary to the displacement, and then $\theta =\text{180º}$ . To reduce the kinetic energy of the parcel to zero, the piece of work ${W}_{\text{fr}}$ past friction must exist minus the kinetic energy that the package started with plus what the package accumulated due to the pushing. Thus ${W}_{\text{fr}}=-\text{95}\text{.}\text{75 J}$ . Furthermore, ${W}_{\text{fr}}=fd\prime \phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta \phantom{\rule{0.25em}{0ex}}\text{= -}fd\prime$ , where $d\prime$ is the altitude information technology takes to stop. Thus,

$d\prime =-\frac{{W}_{\text{fr}}}{f}=-\frac{-\text{95.75 J}}{\text{5.00 N}},$

and then

$d\prime =\text{19}\text{.2 m}.$

Discussion

This is a reasonable altitude for a package to coast on a relatively friction-free conveyor system. Annotation that the work done by friction is negative (the force is in the opposite direction of motion), so it removes the kinetic energy.

Some of the examples in this department tin can be solved without considering energy, but at the expense of missing out on gaining insights about what work and energy are doing in this situation. On the whole, solutions involving energy are more often than not shorter and easier than those using kinematics and dynamics alone.

Section Summary

Conceptual Questions

The person in (Effigy) does work on the lawn mower. Under what conditions would the mower proceeds energy? Under what weather condition would information technology lose free energy?

A person pushing a lawn mower with a force F. Force is represented by a vector making an angle theta below the horizontal and distance moved by the mover is represented by vector d. The component of vector F along vector d is F cosine theta. Work done by the person, W, is equal to F d cosine theta.

Work done on a system puts energy into it. Work washed by a system removes energy from it. Give an example for each statement.

When solving for speed in (Figure), nosotros kept only the positive root. Why?

Problems & Exercises

Compare the kinetic energy of a 20,000-kg truck moving at 110 km/h with that of an eighty.0-kg astronaut in orbit moving at 27,500 km/h.

$1/\text{250}$

(a) How fast must a 3000-kg elephant motion to have the same kinetic energy as a 65.0-kg sprinter running at ten.0 g/s? (b) Discuss how the larger energies needed for the movement of larger animals would relate to metabolic rates.

Confirm the value given for the kinetic energy of an aircraft carrier in (Effigy). Yous will need to look up the definition of a nautical mile (1 knot = 1 nautical mile/h).

$1\text{.}1×{\text{10}}^{\text{10}}\phantom{\rule{0.20em}{0ex}}\text{J}$

(a) Summate the forcefulness needed to bring a 950-kg car to rest from a speed of ninety.0 km/h in a distance of 120 m (a fairly typical distance for a non-panic cease). (b) Suppose instead the car hits a concrete abutment at total speed and is brought to a stop in ii.00 m. Summate the strength exerted on the car and compare it with the force found in part (a).

A automobile's bumper is designed to withstand a 4.0-km/h (1.1-m/s) collision with an immovable object without damage to the trunk of the machine. The bumper cushions the shock by arresting the force over a distance. Calculate the magnitude of the average force on a bumper that collapses 0.200 g while bringing a 900-kg car to rest from an initial speed of 1.1 m/s.

$2\text{.}8×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{N}$

Boxing gloves are padded to lessen the force of a accident. (a) Calculate the force exerted by a boxing glove on an opponent'due south face, if the glove and face shrink seven.50 cm during a blow in which the vii.00-kg arm and glove are brought to rest from an initial speed of 10.0 m/s. (b) Summate the forcefulness exerted by an identical accident in the days when no gloves were used and the duke and face would shrink only two.00 cm. (c) Discuss the magnitude of the force with glove on. Does it seem loftier enough to cause damage even though it is lower than the force with no glove?

Using energy considerations, summate the average force a 60.0-kg sprinter exerts astern on the runway to accelerate from 2.00 to viii.00 m/s in a distance of 25.0 m, if he encounters a headwind that exerts an average force of 30.0 Due north against him.

102 N