How To Find Point Estimate Of Population Proportion

Confidence Intervals

A Population Proportion

During an election year, we see articles in the paper that state conviction intervals in terms of proportions or percentages. For example, a poll for a particular candidate running for president might show that the candidate has twoscore% of the vote within iii percentage points (if the sample is large enough). Often, election polls are calculated with 95% confidence, so, the pollsters would be 95% confident that the true proportion of voters who favored the candidate would exist betwixt 0.37 and 0.43: (0.40 – 0.03,0.twoscore + 0.03).

Investors in the stock market are interested in the truthful proportion of stocks that get upward and down each week. Businesses that sell personal computers are interested in the proportion of households in the United States that own personal computers. Confidence intervals tin can be calculated for the true proportion of stocks that go up or down each week and for the true proportion of households in the U.s.a. that own personal computers.

The procedure to find the confidence interval, the sample size, the error bound, and the confidence level for a proportion is similar to that for the population mean, but the formulas are unlike.

How do you know you are dealing with a proportion problem? Offset, the underlying distribution is a binomial distribution. (There is no mention of a mean or average.) If Ten is a binomial random variable, and so 10 ~ B(n, p) where n is the number of trials and p is the probability of a success. To form a proportion, take Ten, the random variable for the number of successes and divide information technology by northward, the number of trials (or the sample size). The random variable P′ (read "P prime") is that proportion,

${P}^{\prime }=\frac{X}{n}$

(Sometimes the random variable is denoted as $\stackrel{^}{P}$ , read "P hat".)

When n is large and p is not close to nada or 1, nosotros tin can use the normal distribution to guess the binomial.

$X~N\left(np,\sqrt{npq}\right)$

If nosotros divide the random variable, the mean, and the standard deviation past n, we become a normal distribution of proportions with P′, called the estimated proportion, as the random variable. (Recollect that a proportion as the number of successes divided by due north.)

$\frac{X}{n}={P}^{\prime }\text{~ }N\left(\frac{np}{n},\frac{\sqrt{npq}}{n}\right)$

Using algebra to simplify : $\frac{\sqrt{npq}}{n}=\sqrt{\frac{pq}{n}}$

P′ follows a normal distribution for proportions: $\frac{X}{n}={P}^{\prime }\text{~ }N\left(\frac{np}{n},\frac{\sqrt{npq}}{n}\right)$

The confidence interval has the form (p′ – EBP, p′ + EBP). EBP is fault bound for the proportion.

p′ = $\frac{x}{n}$

p′ = the estimated proportion of successes (p′ is a indicate guess for p, the true proportion.)

ten = the number of successes

n = the size of the sample

The mistake bound for a proportion is

$EBP=\left({z}_{\frac{\alpha }{2}}\right)\left(\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}\right)$ where q′ = one – p′

This formula is similar to the fault bound formula for a mean, except that the "advisable standard deviation" is different. For a mean, when the population standard divergence is known, the appropriate standard deviation that we use is $\frac{\sigma }{\sqrt{n}}$ . For a proportion, the appropriate standard deviation is $\sqrt{\frac{pq}{n}}$ .

Notwithstanding, in the fault leap formula, we use $\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}$ as the standard deviation, instead of $\sqrt{\frac{pq}{n}}$ .

In the fault bound formula, the sample proportions p′ and q′ are estimates of the unknown population proportions p and q . The estimated proportions p′ and q′ are used because p and q are not known. The sample proportions p′ and q′ are calculated from the data: p′ is the estimated proportion of successes, and q′ is the estimated proportion of failures.

The confidence interval can be used only if the number of successes np′ and the number of failures nq′ are both greater than five.

Note

For the normal distribution of proportions, the z-score formula is equally follows.

If ${P}^{\prime }\text{~}N\left(p,\sqrt{\frac{pq}{n}}\right)$ then the z-score formula is $z=\frac{{p}^{\prime }-p}{\sqrt{\frac{pq}{n}}}$

Suppose that a market place enquiry firm is hired to estimate the percent of adults living in a large city who have cell phones. 5 hundred randomly selected adult residents in this metropolis are surveyed to determine whether they have cell phones. Of the 500 people surveyed, 421 responded yes – they own cell phones. Using a 95% confidence level, compute a confidence interval estimate for the true proportion of adult residents of this metropolis who have cell phones.

Solution A

The showtime solution is step-by-step (Solution A).
The 2nd solution uses a part of the TI-83, 83+ or 84 calculators (Solution B).

Permit 10 = the number of people in the sample who take cell phones. X is binomial. $X~B\left(500,\frac{421}{500}\right)$ .

To summate the conviction interval, you lot must find p′, q′, and EBP.

north = 500

x = the number of successes = 421

${p}^{\prime }=\frac{x}{n}=\frac{421}{500}=0.842$

p′ = 0.842 is the sample proportion; this is the point approximate of the population proportion.

q′ = 1 – p′ = 1 – 0.842 = 0.158

Since CL = 0.95, then α = one – CL = i – 0.95 = 0.05 $\left(\frac{\alpha }{2}\right)$ = 0.025.

And so ${z}_{\frac{\alpha }{2}}={z}_{0.025}=1.96$

Utilize the TI-83, 83+, or 84+ calculator command invNorm(0.975,0,1) to find z_0.025 . Call back that the area to the right of z_0.025 is 0.025 and the area to the left of z_0.025 is 0.975. This can besides exist establish using advisable commands on other calculators, using a computer, or using a Standard Normal probability table.

$EBP=\left({z}_{\frac{\alpha }{2}}\right)\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}=\left(1.96\right)\sqrt{\frac{\left(0.842\right)\left(0.158\right)}{500}}=0.032$

$p\text{'}-EBP=0.842-0.032=0.81$

${p}^{\prime }+EBP=0.842+0.032=0.874$

The confidence interval for the true binomial population proportion is (p′ – EBP, p′ + EBP) = (0.810, 0.874).

EstimationNosotros guess with 95% confidence that between 81% and 87.4% of all adult residents of this metropolis have cell phones.

Explanation of 95% Confidence LevelXc-five percent of the conviction intervals constructed in this fashion would contain the true value for the population proportion of all adult residents of this city who take prison cell phones.

Solution B

Press STAT and arrow over to TESTS.
Arrow down to A:1-PropZint. Press ENTER.
Pointer down to $x$ and enter 421.
Arrow downwards to $n$ and enter 500.
Arrow down to C-Level and enter .95.
Pointer down to Calculate and press ENTER.
The confidence interval is (0.81003, 0.87397).

Try It

Suppose 250 randomly selected people are surveyed to determine if they own a tablet. Of the 250 surveyed, 98 reported owning a tablet. Using a 95% confidence level, compute a confidence interval estimate for the true proportion of people who ain tablets.

For a class projection, a political scientific discipline pupil at a large academy wants to judge the percent of students who are registered voters. He surveys 500 students and finds that 300 are registered voters. Compute a 90% confidence interval for the true percentage of students who are registered voters, and interpret the confidence interval.

The kickoff solution is step-by-step (Solution A).
The 2nd solution uses a function of the TI-83, 83+, or 84 calculators (Solution B).

Solution A x = 300 and n = 500

${p}^{\prime }=\frac{x}{n}=\frac{300}{500}=0.600$

${q}^{\prime }=1-{p}^{\prime }=1-0.600=0.400$

Since CL = 0.90, then α = 1 – CL = i – 0.ninety = 0.10 $\left(\frac{\alpha }{2}\right)$ = 0.05

${z}_{\frac{\alpha }{2}}$ = z _0.05 = 1.645

Use the TI-83, 83+, or 84+ calculator command invNorm(0.95,0,i) to find z_0.05 . Remember that the area to the right of z_0.05 is 0.05 and the surface area to the left of z_0.05 is 0.95. This tin can also be establish using appropriate commands on other calculators, using a reckoner, or using a standard normal probability table.

$EBP=\left({z}_{\frac{\alpha }{2}}\right)\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}=\left(1.645\right)\sqrt{\frac{\left(0.60\right)\left(0.40\right)}{500}}=0.036$

${p}^{\prime }-EBP=0.60-0.036=0.564$

${p}^{\prime }+EBP=0.60+0.036=0.636$

The confidence interval for the true binomial population proportion is (p′ – EBP, p′ + EBP) = (0.564,0.636).

Interpretation

We estimate with 90% confidence that the true percent of all students that are registered voters is between 56.4% and 63.vi%.
Alternate Wording: We gauge with xc% confidence that between 56.4% and 63.6% of ALL students are registered voters.

Explanation of 90% Confidence LevelNinety percent of all confidence intervals synthetic in this mode contain the true value for the population percent of students that are registered voters.

Solution B

Press STAT and pointer over to TESTS.
Arrow downwards to A:1-PropZint. Press ENTER.
Arrow downwardly to $x$ and enter 300.
Arrow down to $n$ and enter 500.
Pointer down to C-Level and enter 0.90.
Arrow down to Calculate and press ENTER.
The confidence interval is (0.564, 0.636).

Try Information technology

A educatee polls his school to come across if students in the school commune are for or against the new legislation regarding school uniforms. She surveys 600 students and finds that 480 are against the new legislation.

a. Compute a 90% confidence interval for the truthful pct of students who are against the new legislation, and translate the conviction interval.

b. In a sample of 300 students, 68% said they ain an iPod and a smart telephone. Compute a 97% confidence interval for the true percent of students who own an iPod and a smartphone.

"Plus Four" Confidence Interval for p

In that location is a certain corporeality of mistake introduced into the process of calculating a confidence interval for a proportion. Because we do not know the true proportion for the population, we are forced to apply point estimates to calculate the appropriate standard deviation of the sampling distribution. Studies accept shown that the resulting estimation of the standard deviation tin be flawed.

Fortunately, in that location is a simple adjustment that allows us to produce more authentic confidence intervals. We but pretend that we have iv additional observations. Two of these observations are successes and 2 are failures. The new sample size, then, is due north + iv, and the new count of successes is x + 2.

Computer studies accept demonstrated the effectiveness of this method. Information technology should be used when the confidence level desired is at to the lowest degree 90% and the sample size is at least ten.

A random sample of 25 statistics students was asked: "Have you smoked a cigarette in the past calendar week?" Half dozen students reported smoking within the past week. Use the "plus-iv" method to find a 95% conviction interval for the true proportion of statistics students who smoke.

Solution ASix students out of 25 reported smoking within the by calendar week, so x = 6 and due north = 25. Considering we are using the "plus-iv" method, we volition apply 10 = 6 + 2 = viii and n = 25 + 4 = 29.

${p}^{\prime }=\frac{x}{n}=\frac{8}{29}\approx 0.276$

${q}^{\prime }=1-{p}^{\prime }=1-0.276=0.724$

Since CL = 0.95, we know α = 1 – 0.95 = 0.05 and $\frac{\alpha }{2}$ = 0.025.

${z}_{0.025}=1.96$

$EPB=\left({z}_{\frac{\alpha }{2}}\right)\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}=\left(1.96\right)\sqrt{\frac{0.276\left(0.724\right)}{29}}\approx 0.163$

p′ – EPB = 0.276 – 0.163 = 0.113

p′ + EPB = 0.276 + 0.163 = 0.439

We are 95% confident that the true proportion of all statistics students who smoke cigarettes is betwixt 0.113 and 0.439.

Solution B

Press STAT and arrow over to TESTS.
Arrow down to A:one-PropZint. Printing ENTER.

Reminder

Remember that the plus-four method presume an additional four trials: two successes and two failures. Yous do not need to change the procedure for calculating the confidence interval; simply update the values of x and n to reflect these additional trials.

Pointer downwardly to x and enter eight.
Arrow down to n and enter 29.
Arrow downwards to C-Level and enter 0.95.
Pointer downwards to Calculate and printing ENTER.
The confidence interval is (0.113, 0.439).

Try It

Out of a random sample of 65 freshmen at State University, 31 students have alleged a major. Use the "plus-4" method to observe a 96% confidence interval for the truthful proportion of freshmen at State Academy who accept alleged a major.

The Berkman Eye for Net & Social club at Harvard recently conducted a study analyzing the privacy management habits of teen internet users. In a group of 50 teens, 13 reported having more 500 friends on Facebook. Utilize the "plus four" method to discover a 90% confidence interval for the true proportion of teens who would study having more than 500 Facebook friends.

Solution AUsing "plus-four," nosotros have x = xiii + ii = xv and northward = 50 + iv = 54.

${p}^{\text{'}}=\frac{15}{54}\approx 0.278$

${q}^{\text{'}}=1-{p}^{\text{'}}=1-0.241=0.722$

Since CL = 0.90, we know α = 1 – 0.xc = 0.10 and $\frac{\alpha }{2}$ = 0.05.

${z}_{0.05}=1.645$

$EPB=\left({z}_{\frac{\alpha }{2}}\right)\left(\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}\right)=\left(1.645\right)\left(\sqrt{\frac{\left(0.278\right)\left(0.722\right)}{54}}\right)\approx 0.100$

p′ – EPB = 0.278 – 0.100 = 0.178

p′ + EPB = 0.278 + 0.100 = 0.378

Nosotros are ninety% confident that between 17.8% and 37.8% of all teens would report having more than 500 friends on Facebook.

Solution B

Printing STAT and arrow over to TESTS.
Arrow down to A:1-PropZint. Press ENTER.
Arrow down to ten and enter 15.
Arrow down to n and enter 54.
Arrow down to C-Level and enter 0.90.
Arrow down to Calculate and press ENTER.
The confidence interval is (0.178, 0.378).

Try It

The Berkman Heart Study referenced in (Figure) talked to teens in smaller focus groups, simply also interviewed additional teens over the phone. When the written report was consummate, 588 teens had answered the question virtually their Facebook friends with 159 maxim that they have more than than 500 friends. Use the "plus-iv" method to find a 90% confidence interval for the true proportion of teens that would written report having more than than 500 Facebook friends based on this larger sample. Compare the results to those in (Figure).

Calculating the Sample Size due north

If researchers want a specific margin of fault, and so they can use the error spring formula to calculate the required sample size.

The error jump formula for a population proportion is

Suppose a mobile phone company wants to make up one's mind the current percentage of customers aged 50+ who use text messaging on their cell phones. How many customers anile 50+ should the company survey in social club to be ninety% confident that the estimated (sample) proportion is within three pct points of the true population proportion of customers aged 50+ who use text messaging on their cell phones.

From the problem, we know that EBP = 0.03 (3%=0.03) and ${z}_{\frac{\alpha }{2}}$ z _0.05 = i.645 because the confidence level is ninety%.

Still, in social club to find north, nosotros need to know the estimated (sample) proportion p′. Recollect that q′ = 1 – p′. But, we do not know p′ yet. Since we multiply p′ and q′ together, we make them both equal to 0.5 because p′q′ = (0.5)(0.v) = 0.25 results in the largest possible product. (Effort other products: (0.6)(0.four) = 0.24; (0.iii)(0.7) = 0.21; (0.2)(0.viii) = 0.16 and then on). The largest possible product gives us the largest due north. This gives us a big plenty sample then that we can be ninety% confident that we are within three percent points of the true population proportion. To calculate the sample size n, use the formula and make the substitutions.

$n=\frac{{z}^{2}{p}^{\prime }{q}^{\prime }}{EB{P}^{2}}$ gives $n=\frac{{1.645}^{2}\left(0.5\right)\left(0.5\right)}{{0.03}^{2}}=751.7$

Round the answer to the next higher value. The sample size should exist 752 jail cell telephone customers aged fifty+ in gild to be 90% confident that the estimated (sample) proportion is within three percentage points of the true population proportion of all customers aged 50+ who use text messaging on their cell phones.

Endeavour It

Suppose an net marketing company wants to make up one's mind the current percentage of customers who click on ads on their smartphones. How many customers should the visitor survey in order to exist ninety% confident that the estimated proportion is inside 5 percentage points of the truthful population proportion of customers who click on ads on their smartphones?

Chapter Review

Some statistical measures, similar many survey questions, measure qualitative rather than quantitative data. In this case, the population parameter being estimated is a proportion. It is possible to create a confidence interval for the true population proportion post-obit procedures similar to those used in creating conviction intervals for population means. The formulas are slightly different, but they follow the same reasoning.

Let p′ represent the sample proportion, x/n, where x represents the number of successes and n represents the sample size. Let q′ = 1 – p′. And so the confidence interval for a population proportion is given by the following formula:

(lower bound, upper bound) $=\left({p}^{\prime }-EBP,{p}^{\prime } +EBP\right)= \left({p}^{\prime }-z\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}},{p}^{\prime }+z\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}\right)$

The "plus four" method for calculating confidence intervals is an attempt to balance the error introduced by using estimates of the population proportion when computing the standard deviation of the sampling distribution. Simply imagine four additional trials in the study; two are successes and two are failures. Calculate ${p}^{\prime }=\frac{x+2}{n+4}$ , and proceed to observe the confidence interval. When sample sizes are small, this method has been demonstrated to provide more than accurate confidence intervals than the standard formula used for larger samples.

Formula Review

p′ = x / n where x represents the number of successes and n represents the sample size. The variable p′ is the sample proportion and serves equally the betoken estimate for the true population proportion.

q′ = 1 – p′

${p}^{\prime }~N\left(p,\sqrt{\frac{pq}{n}}\right)$ The variable p′ has a binomial distribution that can be approximated with the normal distribution shown here.

EBP = the mistake jump for a proportion = ${z}_{\frac{\alpha }{2}}\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}$

Confidence interval for a proportion:

$\left(\text{lower bound, upper bound)}=\left({p}^{\prime }-EBP,{p}^{\prime }+EBP\right)=\left({p}^{\prime }-z\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}, {p}^{\prime }+z\sqrt{\frac{{p}^{\prime }{q}^{\prime }}{n}}\right)$

$n= \frac{{z}_{\frac{\alpha }{2}}{}^{2}{p}^{\prime }{q}^{\prime }}{EB{P}^{2}}$ provides the number of participants needed to estimate the population proportion with confidence ane – α and margin of error EBP.

Use the normal distribution for a single population proportion $p\prime =\frac{x}{n}$

$EBP=\left({z}_{\frac{\alpha }{2}}\right)\sqrt{\frac{p\prime q\prime }{n}} p\prime +q\prime =1$

The conviction interval has the format (p′ – EBP, p′ + EBP).

$\overline{x}$ is a point estimate for μ

p′ is a point estimate for ρ

due south is a betoken estimate for σ

Use the following information to answer the next ii exercises: Marketing companies are interested in knowing the population percentage of women who make the majority of household purchasing decisions.

When designing a study to determine this population proportion, what is the minimum number yous would demand to survey to be 90% confident that the population proportion is estimated to within 0.05?

If information technology were later determined that it was important to be more than than 90% confident and a new survey were deputed, how would it bear upon the minimum number you need to survey? Why?

Information technology would decrease, because the z-score would subtract, which reducing the numerator and lowering the number.

Use the following information to answer the next five exercises: Suppose the marketing company did do a survey. They randomly surveyed 200 households and found that in 120 of them, the adult female made the bulk of the purchasing decisions. We are interested in the population proportion of households where women make the majority of the purchasing decisions.

Identify the post-obit:

x = ______
n = ______
p′ = ______

Define the random variables 10 and P′ in words.

X is the number of "successes" where the adult female makes the majority of the purchasing decisions for the household. P′ is the pct of households sampled where the woman makes the majority of the purchasing decisions for the household.

Which distribution should you use for this problem?

Construct a 95% conviction interval for the population proportion of households where the women make the majority of the purchasing decisions. Country the confidence interval, sketch the graph, and calculate the error bound.

CI: (0.5321, 0.6679)

This is a normal distribution curve. The peak of the curve coincides with the point 0.6 on the horizontal axis. A central region is shaded between points 0.5321 and 0.6679.

EBM: 0.0679

List two difficulties the company might have in obtaining random results, if this survey were done by email.

Use the post-obit information to respond the side by side 5 exercises: Of 1,050 randomly selected adults, 360 identified themselves equally manual laborers, 280 identified themselves every bit non-manual wage earners, 250 identified themselves equally mid-level managers, and 160 identified themselves as executives. In the survey, 82% of manual laborers preferred trucks, 62% of non-manual wage earners preferred trucks, 54% of mid-level managers preferred trucks, and 26% of executives preferred trucks.

We are interested in finding the 95% confidence interval for the per centum of executives who prefer trucks. Ascertain random variables Ten and P′ in words.

X is the number of "successes" where an executive prefers a truck. P′ is the percentage of executives sampled who prefer a truck.

Which distribution should yous use for this problem?

Construct a 95% confidence interval. Country the confidence interval, sketch the graph, and calculate the error bound.

CI: (0.19432, 0.33068)

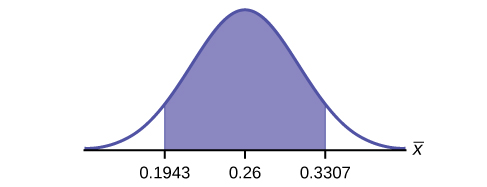
This is a normal distribution curve. The peak of the curve coincides with the point 0.26 on the horizontal axis. A central region is shaded between points 0.1943 and 0.3307.

EBM: 0.0707

Suppose we want to lower the sampling error. What is 1 way to accomplish that?

The sampling error given in the survey is ±2%. Explain what the ±2% means.

The sampling fault ways that the truthful hateful can be two% above or below the sample mean.

Use the post-obit information to answer the next five exercises: A poll of 1,200 voters asked what the well-nigh pregnant issue was in the upcoming election. Sixty-five percent answered the economy. We are interested in the population proportion of voters who feel the economy is the well-nigh important.

Define the random variable X in words.

Define the random variable P′ in words.

P′ is the proportion of voters sampled who said the economy is the most important outcome in the upcoming election.

Which distribution should you use for this problem?

Construct a xc% confidence interval, and state the conviction interval and the error bound.

CI: (0.62735, 0.67265)

EBM: 0.02265

What would happen to the confidence interval if the level of conviction were 95%?

Use the post-obit information to answer the next 16 exercises: The Ice Chalet offers dozens of different beginning ice-skating classes. All of the class names are put into a bucket. The 5 P.Chiliad., Mon night, ages 8 to 12, outset water ice-skating class was picked. In that form were 64 girls and 16 boys. Suppose that we are interested in the true proportion of girls, ages eight to 12, in all get-go ice-skating classes at the Ice Chalet. Assume that the children in the selected class are a random sample of the population.

What is beingness counted?

The number of girls, ages viii to 12, in the 5 P.1000. Monday night beginning water ice-skating class.

In words, define the random variable X.

Summate the following:

x = _______
n = _______
p′ = _______

x = 64
n = 80
p′ = 0.8

State the estimated distribution of X. X~________

Define a new random variable P′. What is p′ estimating?

In words, define the random variable P′.

State the estimated distribution of P′. Construct a 92% Conviction Interval for the true proportion of girls in the ages 8 to 12 get-go ice-skating classes at the Ice Chalet.

${P}^{\prime }~N\left(0.8,\sqrt{\frac{\left(0.8\right)\left(0.2\right)}{80}}\right)$ . (0.72171, 0.87829).

How much area is in both tails (combined)?

How much expanse is in each tail?

0.04

Calculate the following:

lower limit
upper limit
error bound

The 92% confidence interval is _______.

(0.72; 0.88)

Make full in the blanks on the graph with the areas, upper and lower limits of the confidence interval, and the sample proportion.

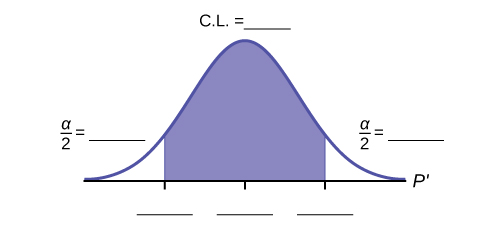
Normal distribution curve with two vertical upward lines from the x-axis to the curve. The confidence interval is between these two lines. The residual areas are on either side.

In 1 complete sentence, explain what the interval ways.

With 92% confidence, we estimate the proportion of girls, ages 8 to 12, in a get-go ice-skating class at the Ice Chalet to exist between 72% and 88%.

Using the same p′ and level of conviction, suppose that n were increased to 100. Would the fault bound become larger or smaller? How do you know?

Using the aforementioned p′ and n = 80, how would the error bound change if the conviction level were increased to 98%? Why?

The error bound would increase. Bold all other variables are kept constant, as the confidence level increases, the surface area under the bend corresponding to the conviction level becomes larger, which creates a wider interval and thus a larger error.

If you decreased the allowable mistake spring, why would the minimum sample size increment (keeping the same level of confidence)?

Homework

Insurance companies are interested in knowing the population pct of drivers who always buckle up earlier riding in a machine.

When designing a study to determine this population proportion, what is the minimum number you would need to survey to exist 95% confident that the population proportion is estimated to inside 0.03?
If it were later determined that it was important to be more than than 95% confident and a new survey was commissioned, how would that bear on the minimum number you would demand to survey? Why?

ane,068
The sample size would need to exist increased since the critical value increases equally the confidence level increases.

Suppose that the insurance companies did do a survey. They randomly surveyed 400 drivers and institute that 320 claimed they always buckle up. We are interested in the population proportion of drivers who claim they ever buckle up.

1. x = __________
2. n = __________
3. p′ = __________
Define the random variables X and P′, in words.
Which distribution should you utilize for this problem? Explain your selection.
Construct a 95% conviction interval for the population proportion who claim they always buckle upward.
1. Country the confidence interval.
2. Sketch the graph.
3. Calculate the mistake spring.
If this survey were done by telephone, list three difficulties the companies might have in obtaining random results.

Co-ordinate to a recent survey of 1,200 people, 61% feel that the president is doing an acceptable job. We are interested in the population proportion of people who feel the president is doing an acceptable job.

Define the random variables X and P′ in words.
Which distribution should you apply for this problem? Explain your selection.
Construct a 90% confidence interval for the population proportion of people who experience the president is doing an acceptable job.
1. Country the confidence interval.
2. Sketch the graph.
3. Calculate the fault bound.

X = the number of people who experience that the president is doing an acceptable chore;

P′ = the proportion of people in a sample who experience that the president is doing an acceptable job.
$N\left(0.61,\sqrt{\frac{\left(0.61\right)\left(0.39\right)}{1200}}\right)$
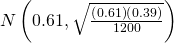
1. CI: (0.59, 0.63)
2. Check pupil's solution
3. EBM: 0.02

An commodity regarding interracial dating and marriage recently appeared in the Washington Postal service. Of the 1,709 randomly selected adults, 315 identified themselves as Latinos, 323 identified themselves as blacks, 254 identified themselves as Asians, and 779 identified themselves as whites. In this survey, 86% of blacks said that they would welcome a white person into their families. Among Asians, 77% would welcome a white person into their families, 71% would welcome a Latino, and 66% would welcome a black person.

We are interested in finding the 95% conviction interval for the percentage of all black adults who would welcome a white person into their families. Define the random variables X and P′, in words.
Which distribution should you use for this problem? Explain your pick.
Construct a 95% conviction interval.
1. State the confidence interval.
2. Sketch the graph.
3. Calculate the error bound.

Refer to the information in (Effigy).

Construct 3 95% conviction intervals.
1. percent of all Asians who would welcome a white person into their families.
2. percent of all Asians who would welcome a Latino into their families.
3. percent of all Asians who would welcome a black person into their families.
Even though the three point estimates are different, do whatever of the confidence intervals overlap? Which?
For any intervals that practise overlap, in words, what does this imply nearly the significance of the differences in the true proportions?
For any intervals that exercise non overlap, in words, what does this imply about the significance of the differences in the true proportions?

1. (0.72, 0.82)
2. (0.65, 0.76)
3. (0.60, 0.72)
Yeah, the intervals (0.72, 0.82) and (0.65, 0.76) overlap, and the intervals (0.65, 0.76) and (0.60, 0.72) overlap.
We can say that there does not appear to be a significant deviation between the proportion of Asian adults who say that their families would welcome a white person into their families and the proportion of Asian adults who say that their families would welcome a Latino person into their families.
We can say that there is a meaning difference between the proportion of Asian adults who say that their families would welcome a white person into their families and the proportion of Asian adults who say that their families would welcome a blackness person into their families.

Stanford University conducted a study of whether running is healthy for men and women over age 50. During the first viii years of the study, ane.5% of the 451 members of the 50-Plus Fitness Association died. We are interested in the proportion of people over 50 who ran and died in the same eight-year period.

Ascertain the random variables X and P′ in words.
Which distribution should y'all use for this problem? Explicate your selection.
Construct a 97% confidence interval for the population proportion of people over 50 who ran and died in the same eight–year flow.
1. Land the confidence interval.
2. Sketch the graph.
3. Calculate the mistake bound.
Explicate what a "97% conviction interval" means for this report.

A phone poll of one,000 adult Americans was reported in an consequence of Fourth dimension Magazine. I of the questions asked was "What is the principal trouble facing the country?" Xx percent answered "crime." We are interested in the population proportion of adult Americans who feel that crime is the main problem.

Ascertain the random variables Ten and P′ in words.
Which distribution should yous use for this problem? Explain your choice.
Construct a 95% confidence interval for the population proportion of developed Americans who feel that offense is the chief problem.
1. State the confidence interval.
2. Sketch the graph.
3. Summate the error bound.
Suppose we want to lower the sampling error. What is ane way to accomplish that?
The sampling error given past Yankelovich Partners, Inc. (which conducted the poll) is ±three%. In ane to three complete sentences, explain what the ±3% represents.

10 = the number of developed Americans who feel that offense is the main problem; P′ = the proportion of adult Americans who experience that crime is the main trouble
Since we are estimating a proportion, given P′ = 0.2 and n = 1000, the distribution we should utilize is $N\left(0.2,\sqrt{\frac{\left(0.2\right)\left(0.8\right)}{1000}}\right)$ .
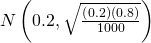1. CI: (0.eighteen, 0.22)
2. Check pupil'due south solution.
3. EBM: 0.02
One style to lower the sampling error is to increase the sample size.
The stated "± 3%" represents the maximum error bound. This means that those doing the study are reporting a maximum error of 3%. Thus, they estimate the percentage of adult Americans who feel that crime is the main problem to be between xviii% and 22%.

Refer to (Figure). Another question in the poll was "[How much are] y'all worried well-nigh the quality of instruction in our schools?" Sixty-three percent responded "a lot". We are interested in the population proportion of adult Americans who are worried a lot nearly the quality of teaching in our schools.

Ascertain the random variables X and P′ in words.
Which distribution should yous use for this trouble? Explicate your selection.
Construct a 95% confidence interval for the population proportion of adult Americans who are worried a lot about the quality of didactics in our schools.
1. State the confidence interval.
2. Sketch the graph.
3. Calculate the error leap.
The sampling mistake given by Yankelovich Partners, Inc. (which conducted the poll) is ±three%. In one to three complete sentences, explain what the ±three% represents.

Apply the post-obit information to reply the next three exercises: According to a Field Poll, 79% of California adults (actual results are 400 out of 506 surveyed) feel that "instruction and our schools" is one of the top issues facing California. We wish to construct a 90% confidence interval for the true proportion of California adults who feel that pedagogy and the schools is one of the top bug facing California.

A point estimate for the true population proportion is:

0.90
i.27
0.79
400

A 90% confidence interval for the population proportion is _______.

(0.761, 0.820)
(0.125, 0.188)
(0.755, 0.826)
(0.130, 0.183)

The error jump is approximately _____.

ane.581
0.791
0.059
0.030

Utilise the following information to answer the adjacent two exercises: V hundred and eleven (511) homes in a certain southern California community are randomly surveyed to determine if they meet minimal earthquake preparedness recommendations. Ane hundred seventy-iii (173) of the homes surveyed met the minimum recommendations for earthquake preparedness, and 338 did not.

Find the confidence interval at the xc% Confidence Level for the truthful population proportion of southern California community homes meeting at to the lowest degree the minimum recommendations for convulsion preparedness.

(0.2975, 0.3796)
(0.6270, 0.6959)
(0.3041, 0.3730)
(0.6204, 0.7025)

The point estimate for the population proportion of homes that do not meet the minimum recommendations for earthquake preparedness is ______.

0.6614
0.3386
173
338

On May 23, 2013, Gallup reported that of the i,005 people surveyed, 76% of U.South. workers believe that they will continue working past retirement age. The confidence level for this study was reported at 95% with a ±3% margin of fault.

Decide the estimated proportion from the sample.
Determine the sample size.
Identify CL and α.
Summate the error leap based on the information provided.
Compare the error spring in part d to the margin of error reported by Gallup. Explicate any differences between the values.
Create a confidence interval for the results of this study.
A reporter is covering the release of this study for a local news station. How should she explain the conviction interval to her audience?

A national survey of one,000 adults was conducted on May 13, 2013 by Rasmussen Reports. It concluded with 95% confidence that 49% to 55% of Americans believe that big-time college sports programs corrupt the process of college pedagogy.

Discover the point gauge and the mistake bound for this confidence interval.
Can we (with 95% conviction) conclude that more than than half of all American adults believe this?
Utilize the bespeak estimate from part a and n = 1,000 to calculate a 75% conviction interval for the proportion of American adults that believe that major college sports programs corrupt higher education.
Can we (with 75% confidence) conclude that at least half of all American adults believe this?

p′ = 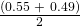$\frac{\text{(0}\text{.55 + 0}\text{.49)}}{\text{2}}$ = 0.52; EBP = 0.55 – 0.52 = 0.03
No, the confidence interval includes values less than or equal to 0.fifty. It is possible that less than half of the population believe this.
CL = 0.75, and so α = 1 – 0.75 = 0.25 and 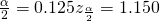$\frac{\alpha }{2}=0.125 {z}_{\frac{\alpha }{2}}=1.150$ . (The area to the right of this z is 0.125, and so the area to the left is one – 0.125 = 0.875.)
$EBP=\left(1.150\right)\sqrt{\frac{0.52\left(0.48\right)}{1,000}}\approx 0.018$
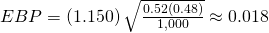
(p′ – EBP, p′ + EBP) = (0.52 – 0.018, 0.52 + 0.018) = (0.502, 0.538)
Alternate Solution

STAT TESTS A: i-PropZinterval with x = (0.52)(one,000), n = 1,000, CL = 0.75.

Answer is (0.502, 0.538)
Yes – this interval does not fall less than 0.50 so nosotros tin can conclude that at least half of all American adults believe that major sports programs corrupt education – merely nosotros practise so with only 75% confidence.

Public Policy Polling recently conducted a survey asking adults across the U.S. about music preferences. When asked, lxxx of the 571 participants admitted that they take illegally downloaded music.

Create a 99% confidence interval for the true proportion of American adults who take illegally downloaded music.
This survey was conducted through automated telephone interviews on May vi and 7, 2013. The fault spring of the survey compensates for sampling error, or natural variability among samples. List some factors that could affect the survey'due south event that are non covered by the margin of mistake.
Without performing whatever calculations, describe how the confidence interval would change if the confidence level inverse from 99% to xc%.

You programme to conduct a survey on your college campus to learn well-nigh the political awareness of students. You desire to approximate the truthful proportion of higher students on your campus who voted in the 2012 presidential election with 95% conviction and a margin of error no greater than five percent. How many students must you interview?

CL = 0.95 α = 1 – 0.95 = 0.05 $\frac{\alpha }{2}$ = 0.025 ${z}_{\frac{\alpha }{2}}$ = 1.96. Use p′ = q′ = 0.v.

$n=\frac{ {z}_{\frac{\alpha }{2}}{}^{2}{p}^{\prime }{q}^{\prime }}{EB{P}^{2}}= \frac{{1.96}^{2}\left(0.5\right)\left(0.5\right)}{{0.05}^{2}}=384.16$

Yous demand to interview at to the lowest degree 385 students to approximate the proportion to within five% at 95% confidence.

In a recent Zogby International Poll, nine of 48 respondents rated the likelihood of a terrorist attack in their customs equally "probable" or "very likely." Utilise the "plus four" method to create a 97% confidence interval for the proportion of American adults who believe that a terrorist assail in their community is likely or very likely. Explain what this confidence interval ways in the context of the problem.

Source: https://opentextbc.ca/introstatopenstax/chapter/a-population-proportion/#:~:text=Formula%20Review,for%20the%20true%20population%20proportion.

Posted by: newtondictiony.blogspot.com